3 закон Кеплера — это один из основополагающих законов в области астрономии. Он был открыт немецким астрономом Иоганном Кеплером в начале 17 века и позволяет описывать движение планет вокруг Солнца. В своих работах Кеплер сформулировал три закона, которые впоследствии получили его имя.
Третий закон Кеплера связывает период обращения планеты вокруг Солнца с ее средним удалением от Солнца. Формула, описывающая этот закон, записывается следующим образом:
T^2 = k * a^3,
где T — период обращения планеты вокруг Солнца, а — среднее удаление планеты от Солнца, k — постоянная, которая зависит от системы единиц измерения.
Значение третьего закона Кеплера заключается в том, что он позволяет описывать период обращения планеты вокруг Солнца, опираясь только на ее среднее удаление от Солнца. Таким образом, с помощью этой формулы можно расчетить период обращения планеты исходя из ее расстояния до Солнца. Это имеет большое значение для астрономии, поскольку позволяет более точно предсказывать движение планет и расстояния между ними в разных точках их орбит.
Закон Кеплера
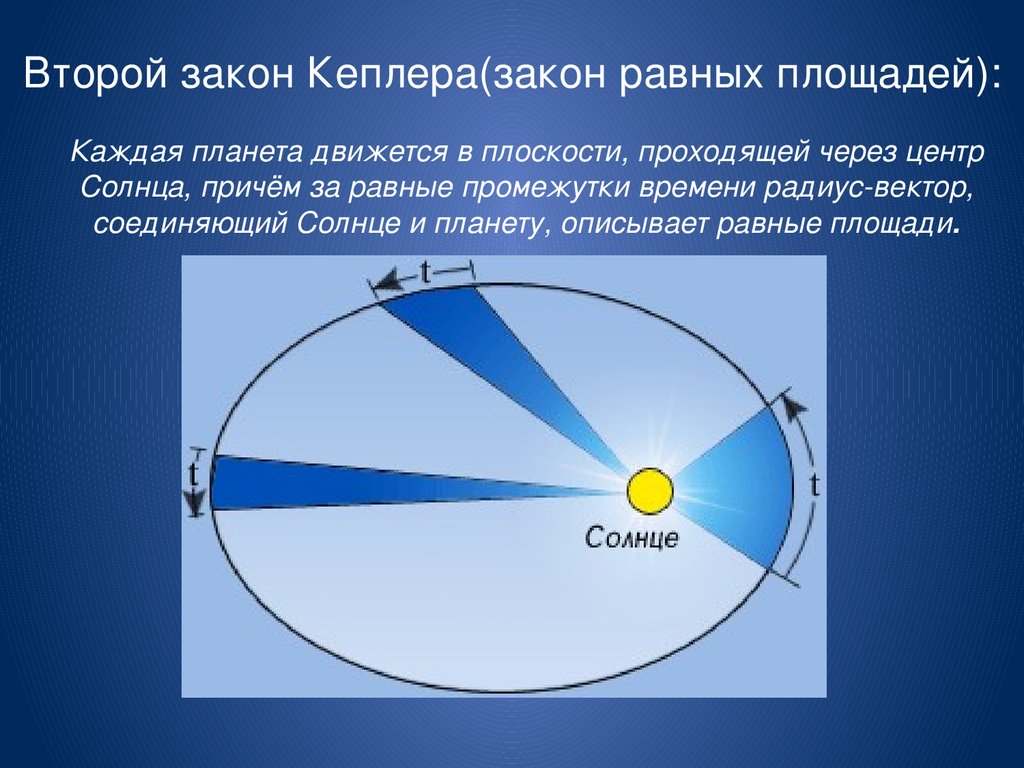
Согласно первому закону Кеплера, планеты движутся по эллиптическим орбитам, в фокусе которых находится Солнце. Второй закон Кеплера говорит о том, что радиус-вектор, соединяющий планету с Солнцем, за равные промежутки времени проходит одинаковые площади. Третий закон, также известный как закон гармонических интервалов, устанавливает связь между периодом обращения планеты вокруг Солнца и полуосью ее орбиты.
Формула третьего закона Кеплера имеет вид: T^2 = k × a^3, где T — период обращения планеты вокруг Солнца, a — полуось орбиты планеты, k — постоянная, зависящая от системы единиц, в которой проводится измерение.
Значение закона Кеплера в орбитальной механике и астрономии трудно переоценить. Он позволяет предсказывать движение планет и спутников, а также использоваться для поиска экзопланет. Закон Кеплера стал важным этапом в развитии астрономии, выступая мостом между античными представлениями о космосе и современной научной картиной мира.
Расчет формулы
Формула, описывающая третий закон Кеплера, устанавливает зависимость между периодом обращения планеты вокруг Солнца и её средним расстоянием до Солнца:
T² = kR³
Где:
- T — период обращения планеты вокруг Солнца (в секундах)
- k — гравитационная постоянная
- R — среднее расстояние планеты до Солнца (в метрах)
Зная значения k и R, можно рассчитать период обращения планеты вокруг Солнца по данной формуле.
Если T — период обращения планеты вокруг Солнца, а r — радиус ее орбиты, то формула будет следующей:
T2 = k r3,
где k — постоянная, которая зависит от массы и суммарного радиуса всех тел, находящихся внутри орбиты данной планеты.
Формула Кеплера позволяет связать период обращения планеты вокруг Солнца с ее орбитальным радиусом. Благодаря этой формуле, астрономы могут определить период обращения планеты, зная ее орбиту, и наоборот.
Формула третьего закона Кеплера позволяет вычислить период обращения планеты вокруг Солнца.
Формула третьего закона Кеплера выглядит следующим образом:
P^2 = a^3
где P обозначает период обращения планеты вокруг Солнца, а a — среднее расстояние от Солнца до планеты.
Использование этой формулы позволяет определить период обращения планеты вокруг Солнца на основе известного среднего расстояния от Солнца до планеты. Таким образом, формула третьего закона Кеплера является важным инструментом для астрономов при изучении планет и их движения вокруг звезды.
Значение закона
Формула третьего закона Кеплера выглядит следующим образом:
- Т^2 = k * a^3
где T — период обращения планеты вокруг Солнца, a — большая полуось орбиты, k — постоянная, которая зависит только от массы и расстояния до Солнца.
Закон Кеплера позволил установить объективные закономерности движения планет в Солнечной системе и является основой для многих астрономических расчетов и прогнозов. Этот закон стал одним из важных шагов в развитии науки об астрономии и помог сформировать современное представление о строении Вселенной.
3 закон Кеплера позволяет определить зависимость между периодом обращения и расстоянием до Солнца.
Согласно 3 закону Кеплера, квадрат периода обращения планеты вокруг Солнца пропорционален кубу большой полуоси эллипса, по которому она движется. Другими словами, чем дальше планета находится от Солнца, тем дольше ей требуется для совершения полного оборота.
Формула, позволяющая рассчитать зависимость между периодом обращения (T) и расстоянием до Солнца (a), выглядит следующим образом:
T^2 = k*a^3
Где T обозначает период обращения планеты (в годах), a — расстояние от планеты до Солнца (в астрономических единицах), k — постоянная, зависящая от массы и гравитационной постоянной.
Значение 3 закона Кеплера заключается в том, что благодаря ему мы можем определить положение планеты в Солнечной системе и предсказать ее движение. Этот закон позволяет устанавливать математические связи между различными планетами и общую систему движения вокруг Солнца.
Закон дает возможность расчета орбитального периода планет на основе их расстояния от Солнца.
Суть закона заключается в пропорциональности кубов расстояний планет от Солнца (больших полуосей их орбит) и квадратов их орбитальных периодов. То есть, когда планеты двигаются по орбитам с различными расстояниями от Солнца, они будут иметь разные орбитальные периоды.
Закон Кеплера позволяет косвенно определить длину орбитального периода планеты, используя формулу:
T2 = k * r3
Где:
- T – орбитальный период планеты
- r – расстояние планеты от Солнца
- k – постоянная, зависящая от характеристик солнечной системы
Таким образом, если известно расстояние от планеты до Солнца, то можно легко вычислить ее орбитальный период, а если известен период, то можно определить расстояние планеты от Солнца.
Это имеет важное значение для астрономии, так как позволяет рассчитать орбитальные периоды планет и других небесных объектов с высокой точностью. Кроме того, этот закон позволяет установить закономерности движения планет и наблюдать их закономерные перемещения на небосводе.
Вопрос-ответ:
Как найти формулу для третьего закона Кеплера?
Формула третьего закона Кеплера (закон гармонических законов) состоит в том, что квадраты периодов обращения планет вокруг Солнца относятся кубически по их средним расстояниям от Солнца. Формула имеет вид: T^2 = k * r^3, где T — период обращения планеты вокруг Солнца, r — среднее расстояние планеты от Солнца, k — постоянная пропорциональности.
Каким образом можно вывести формулу для третьего закона Кеплера?
Формула третьего закона Кеплера может быть выведена с использованием закона всемирного тяготения Ньютона. Из закона всемирного тяготения следует, что сила притяжения между планетой и Солнцем пропорциональна массе планеты и обратно пропорциональна квадрату расстояния между ними. Затем, используя второй закон Ньютона и закон Кеплера о равномерном движении планеты по орбите, можно получить формулу третьего закона Кеплера.
Какое значение имеет формула третьего закона Кеплера?
Формула третьего закона Кеплера позволяет установить соотношение между периодом обращения планеты вокруг Солнца и средним расстоянием планеты от Солнца. Это соотношение помогает установить закономерности в движении планет и предсказывать их движение. Формула также позволяет вычислять период обращения планет и определять их средние расстояния от Солнца, основываясь на известных данных о движении других планет.
Можно ли использовать формулу третьего закона Кеплера для расчета движения спутников?
Да, формула третьего закона Кеплера может быть применена не только к движению планет вокруг Солнца, но и к движению спутников вокруг планет. Она позволяет связать период обращения спутника вокруг планеты с его средним расстоянием от планеты. В сочетании с другими законами Кеплера и законами механики, эта формула может быть использована для расчета и предсказания движения спутников и определения их орбит.
Как можно рассчитать формулу третьего закона Кеплера?
Формула третьего закона Кеплера выражает связь между периодом обращения планеты вокруг Солнца и средним расстоянием между ними. Она имеет следующий вид: P^2 = a^3, где P — период обращения планеты вокруг Солнца (в годах), а — среднее расстояние между планетой и Солнцем (в астрономических единицах).